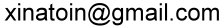Unit conversion
thickness calculation:
object weight in μg/cm2
object density in g/cm3
Result = m.
Result = cm.
Result = um.
note:
μm = 10-6 m
mm = 10-3 m
cm = 10-2 m
As an example, for the 260 μg/cm2 18O target formed by the electrolysis of water enriched 97% in 18O on a 12.7 μm Tantalum backing. The common general compund is Ta2O5 and its density is around 8.2 g/cm3. Ta has atomic mass = 181, and then 260 μg/cm2 O will prodcue 260/(18*5) * (181*2 + 18*5) = 1306 μg/cm2 Ta2O5, and then the thickness is 0.000159 cm.
_ _ _ _ _ _ _ _ _
The numbers of Ta$_{2}$O$_{5}$ in a cube of cm$^{3}$ = NA * density / {a.m.u(Ta)$\times$2 + a.m.u(O)$\times$5}
the unit of a.m.u is equal to [g/mol]
the density is in [g/cm$^{3}$]
NA = Avogadro number = 6.022 $\times$ 10$^{23}$
_ _ _ _ _ _ _ _ _
Suppose we know a reaction has cross-section = cs mb (mini-barn). And then we can estimate the total reaction events from the information of target. 'cross-section' is in the unit of area, and its concept is when the incident particle coming into this effective area then the reaction will happen. For classical cases, if the target is a sphere with radius = $R$, then the cross-section = $ 4\pi R$.
set
cs = $0.1$ mb = $10^{-28}$ cm$^{2}$, for a reaction with $^{18}$O target
n = 5.48$\times$10$^{22}$ = number of $^{18}$O in a cube of cm$^{3}$.
t = 2.44$\times$10$^{-4}$ cm = target thickness
beam_rate = 10$^{7}$ ions/sec
Reaction rate = beam_rate$( 1-exp(-n\cdot cs \cdot t) )$, according to reference(10.4)
roughly speaking we will have 50 events per hour.