'stp_lib' Introduction
stopping power or dE/dx is to describe how a particle loses its energy when it is traveling in a medium. For example, it can be used to estimate how much energy a particle will deposit when it passes through your detector. In nuclear physics, the unit of dE/dx is $\frac{MeV}{mg/cm^{2}}$, since the beam normally in unit of $MeV$, and the target thickness is in unit of $mg/cm^{2}$.
There are several programs can simulate dE/dx for all kinds of particles in a medium. For example, SRIM ( official website) and LISE++ ( official website). However, sometimes, I need to generate dE/dx data for internal use for my program, and reading stopping power from external files is not genuinely convenient. So I search the library that can help me generate dE/dx file, but I don't have any good luck to find it.
I come across that VIKAR program ( Virtual Instrumentation for Kinematics and Reactions, by Dr. S.D. Pain ) has its dE/dx generator, and I have the source code. Not only I would like to study how VIKAR's dE/dx data compares to those from LISE++, but also I would like to extract VIKAR's dE/dx generator. The VIKAR is written in Fortran, and some parts of code is in Fortran 77. The main part for dE/dx calculation is the subroutine ncdedx. I rewrite and simplify the ncdedx subroutine, and translate the code into a C++ class, which provides easy-to-use methods to get the dE/dx and stopping range data.
Run the code:
I prepare two versions. One can be used in ROOT (i.e. using TMath library), and one is just pure c++ for your convenient. You can download the source from my GitHub repository (link) or here
In the following, I will just use the ROOT version to do a quick demo. The case is for $^{86}Kr$ particle to travel in a $CH_{2}$ medium. The class constructor will need 6 pieces of information; three from the target (CH2), and three from the beam. The CH2 target is composed of one carton and two hydrogen. Hence, the average $A = 14/3$, average $Z = 8/3$.
The class name is "stp_class".
to calculate the dEdx data, we invoke process() method.
to get the dEdx, we invoke get_dEdx() method.
to get the range, we invoke get_range() method.
to set the beam energy, we invoke set_beam_energy( eng )
.
// target = CH2
// C ==> A = 12, Z = 6
// H ==> A = 1, Z = 1
// A_avg = ( 12*1 + 1*2) / 3
// Z_avg = ( 6*1 + 1*2) / 3
// beam = 86Kr, A = 86, Z = 36
double target_density = 0.93; // [g/cm^3]
double target_A_avg = 14./3;
double target_Z_avg = 8./3;
double beam_A = 86;
double beam_Z = 36;
double beam_eng = 90; // [MeV]
stp_class* demo_obj;
demo_obj = new stp_class( target_density,
target_A_avg,
target_Z_avg,
beam_A,
beam_Z,
beam_eng );
TGraph* gr = new TGraph();
int pointN = 0;
for( double eng = 1; eng < 5000; eng+=1) {
demo_obj->set_beam_energy( eng );
demo_obj->process();
double dEdx = demo_obj->get_dEdx();
gr->SetPoint( pointN, eng, dEdx ); pointN+=1; }
gr->Draw("APL");
compare the results.
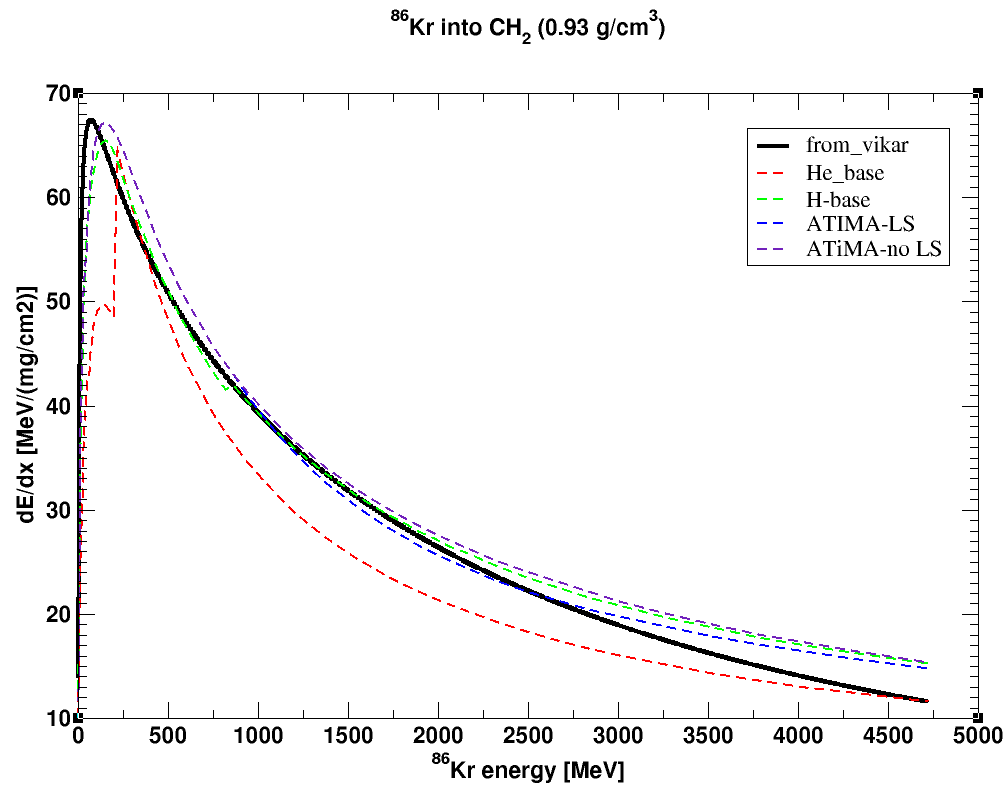
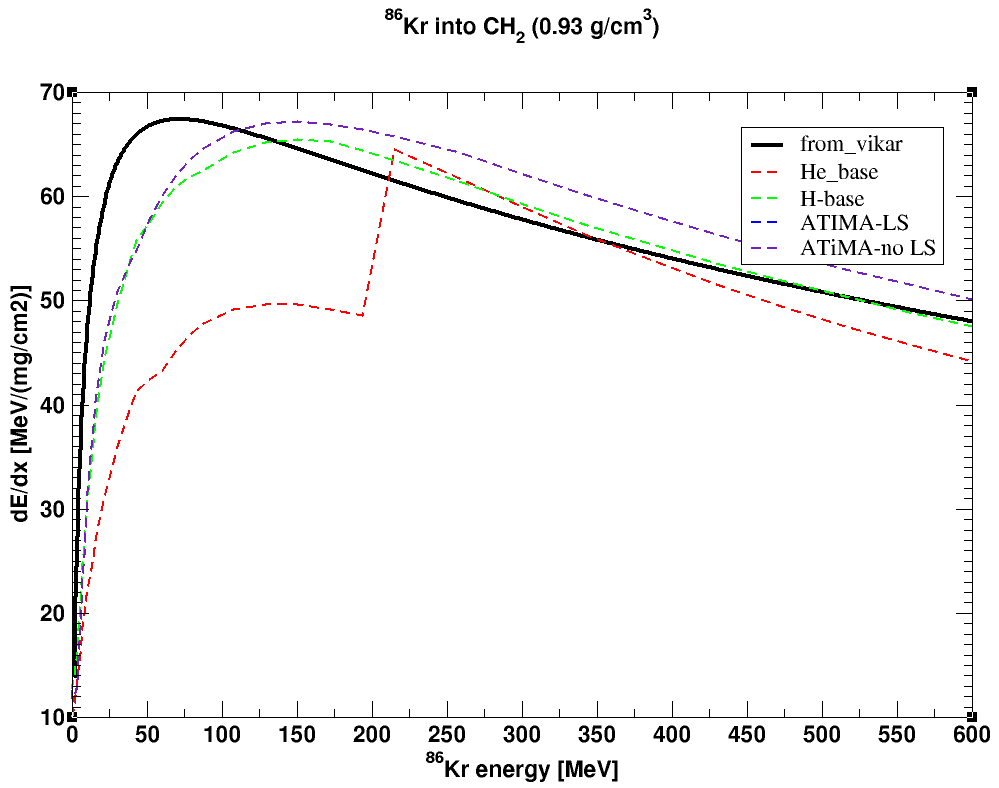
The following are the results of stp_lib which is derived from the ncdedx subroutine of VIKAR program. The curves labeled as "He_base", "H_base", "ATIMA-LS", and "ATIMA-no LS" are from the LISE++ calculations.
The reference:
[He-base] F.Hubert et al, AD&ND Tables 46 (1990) 1
[H -base] J.F.Ziegler et al, Pergamon Press, NY (low energy)
ATIMA 1.2 LS-theory (recommended for high energy)
ATIMA 1.2 without LS-correction
It is clear the dE/dx from VIKAR rises and reach its max too fast ( see the energy under 50 MeV), and it also drops too fast for the higher energy part ( see the energy above 3000 MeV). The good agreement comes at the range between around 1000 to 2000 MeV. If you would like to have precise dE/dx data, I would recommend to use the results from LISE++.