Introduction
Most of the time, when we perform an experiment, we are interested in
the particle's angle and energy ranges after reaction, since we have
to make sure our detectors are able to measure them in these energy and
angle ranges. We also want the information about the CM and Lab frame angle
conversion, since it can help us to compare the results from theories, in which
the CM angles are often used.
We can frame our questions as:
(1) given a lab scattering angle $\psi$, what is the CM scattering angle $\theta$ ?
(2) given a lab scattering angle $\psi$, what is kinematic energy $T_3$ ?
Suppose the Q value of the reaction, $M_1$, $M_2$, $M_3$, $M_4$, and the $T_1$ ( beam energy) are known.
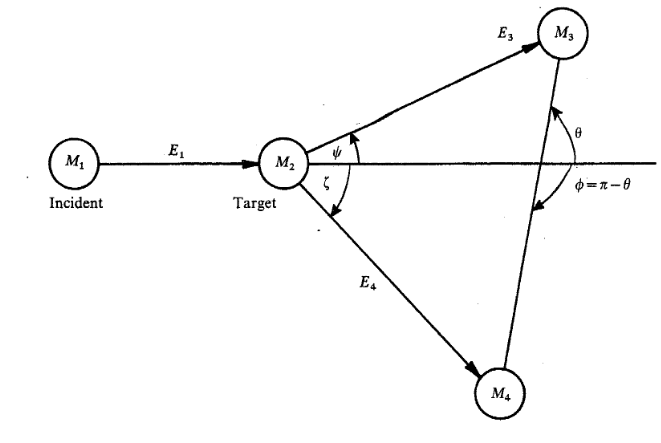
The kinematics can be categorized into three cases:
(a) elastic scattering $M_1$ = $M_3$ ( and $M_2$ = $M_4$ )
(b) $M_3$ > $M_2$, ex. (p,d) type
(c) $M_2$ > $M_3$, ex. (d,p) type
When $M_1$ > $M_2$, we call it as inverse kinematics.
Note: only when inverse KM + (p,d) type reaction, we can have two solutions.
The page only shows the calculation results, for the methods beyond the calculations,
please refer to this page.