The page only shows the formulae for two-boy kinematics, for the the calculation results,
please refer to this page.
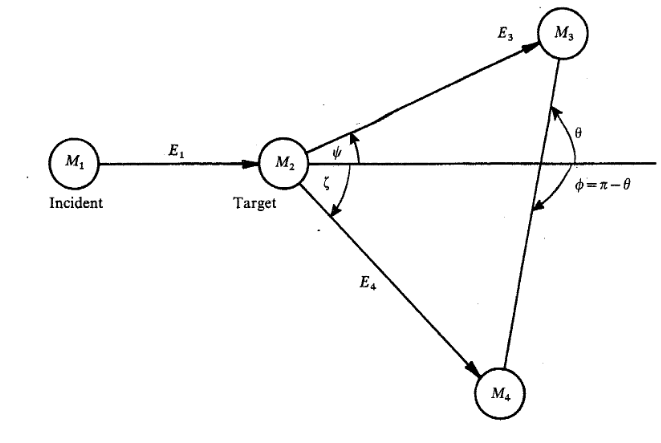
suppose we have a two-body reaction $ 1 + 2 $ → $ 3 + 4 $.
let's define the suffix $1$ is the beam, and the suffix $2$ is the target.
$E = T + m$.
$E^2 = m^2 + p^2$
$T$ stands for kinematic energy [MeV], $m$ is for the mass [MeV/c^2].
$E$ is the energy, and it is the sum of kinematic energy and rest mass.
$p$ is for momentum [MeV/c].
Before the reaction at Lab frame, $E_1 = T_1 + m_1$, and $E_2 = m_2$
(our target is rest. It means $T_2=0$ and $p_2 = 0$).
$E_T$ = total energy = $E_1 + E_2$ = $T_1 + m_1 + m_2$.
The square of the four-vector $(E, \vec{p})$ is invariant under Lorentz transformation.
$s\equiv $ $(E_1+E_2$, $\vec{p_{1}} + \vec{p_{2}} )^2$
note: $(x_0, x_1, x_2, x_3)^2 = x_0^2 -(x_1^2 +x_2^2 +x_3^2)$
since our target is rest, $E_2 = m_2$ and $\vec{p_{2}} = 0$, then:
$s = (E_1+m_2)^2 - p_1^2$
$s = E_1^2 - p_1^2 + m_2^2 + 2 E_1 m_2 $
$s = m_1^2 + m_2^2 + 2 E_1 m_2 $
Let us use a $*$ for the quantity at the CM frame, in which the total linear momentum sum is zero.
Once again, $s$ is invariant under Lorentz transformation, which means $s$ will be all the same either we express the quantity in the CM frame or Lab frame. From the CM frame, we can get :
$s$= $(E_1^* + E_2^*)^2 + (\vec{p^*_{1}} + \vec{p^*_{2}})$,
since the sum of total linear momentum = 0, so
$s$= $(E_1^* + E_2^*)^2 $.
we can re-write the above equation as
$E^*_1 = \sqrt{s} - E^*_2 = \sqrt{ p_1^*2 + m_1^2}$
Then, $s - 2 \sqrt{s} E^*_2 + E^{*2}_2 = p_1^*2 + m_1^2 $
re-arragne: $ 2 \sqrt{s} E^*_2 = s + E^{*2}_2 - p_1^*2 - m_1^2 $
$E^*_2 = \frac{s + p_2*^2 + m_2^2 - p_1^*2 - m_1^2}{2\sqrt{s}}$
Finally,
$E^*_2 = \frac{s + m_2^2 - m_1^2}{2\sqrt{s}}$,
similarly, we can get:
$E^*_1 = \frac{s + m_1^2 - m_2^2}{2\sqrt{s}}$
$E^*_3 = \frac{s + m_3^2 - m_4^2}{2\sqrt{s}}$
$E^*_4 = \frac{s + m_4^2 - m_3^2}{2\sqrt{s}}$
At the same time:
$p_1^* = p_2^* = \sqrt{E_1^{*2} - m_1^2 } = \sqrt{E_2^{*2} - m_2^2 }$
$p_3^* = p_4^* = \sqrt{E_3^{*2} - m_3^2 } = \sqrt{E_4^{*2} - m_4^2 }$
The square of any Four vector is invariant under Lorentz transformation.
This time, we use $t$, which is defined as:
$t \equiv (E_3-E_1$, $\vec{p_{3}} - \vec{p_{1}} )^2$
$t$ is similar to $s$, but we just use particle $1$ and $3$.
$t = (E_3-E_1)^2 - (\vec{p_{3}} - \vec{p_{1}})^2$,
and from energy and momentum conservation, it can be shown that
$t = (E_4-E_2)^2 - (\vec{p_{4}} - \vec{p_{2}})^2$.
$t = E_3^2 + E_1^2 - 2 E_1 E_3 - p_1^2 - p_3^2 + 2\vec{p_{3}}\cdot \vec{p_{1}} $
$t = m_3^2 + m_1^2 + 2 p_1 p_3 \cdot cos(\psi) - 2 E_1 E_3$.
And similarly,
$t = m_4^2 + m_2^2 + 2 p_2 p_4 \cdot cos(\xi) - 2 E_2 E_4$.
Just a reminder: $\psi$ is the lab frame scattering angle of particle $3$. In the CM frame, it is $\theta$.
$\xi$ is the lab frame scattering angle of particle $4$.
In the CM frame, it is $\phi = \pi - \theta$.
When particle $2$ is rest, its $p_2 = 0$,
$t = m_4^2 + m_2^2 - 2 E_2 E_4$
In the Lab and CM frame $t$ will have the same expression,
so we can arrange the terms as:.
$ cos(\theta) = (t - m_3^2 - m_1^2 + 2 E_1^* E_3^*)/(2 p_1 p_3)$.
so, once we know $E_4$ for a given $\psi$, we can calculate $t$ and $\theta$.
In the following, I summarize how to get $E_3$ and $E_4$
The reference is from page 140 of "Nuclear Reaction Analysis" by Maryon Young.
$A \equiv 2 m_2 T_1 + 2 m_1 m_3 + 2 m_2 m_3 + 2 Q (m_1 + m_2 - m_3) -Q^2$
$B \equiv E_T^2 - p_1 \cdot cos^2(\psi) $
Just a reminder: $Q$ is the reaction q value, and $E_T = T_1 + m_1 + m_2 = E_1 + E_2$,
and $\psi$ is the lab angle of outgoing particle $3$, which normally is detected by our detectors.
$E_3 = \frac{1}{B} \{ E_T\cdot A \pm p_1\cdot cos(\psi) \sqrt{A^2-4 m_3^2 B} \} $
$E_4 = E_T - E_3$
For elastic scattering, it is easier.
just a reminder, $\xi$ is the target scattering angle in the Lab frame,
and $\phi$ is the target scattering angle in the CM frame.
$\psi$ is the beam scattering angle in the Lab frame.
$\theta$ is the beam scattering angle in the CM frame.
Given a $\theta$, we can get :
$\phi = 180 - \theta$.
$\xi = \phi/2$.
$\psi = atan( \frac{ sin(2\xi) }{ m_1/m_2 - cos(2\xi) })$.
$T_4 + T_3 = T_1$.
$T_3 / T_1 = 1 - \frac{2 m_1 m_2}{(m_1+m_2)^2}\cdot(1-cos(\theta))$.