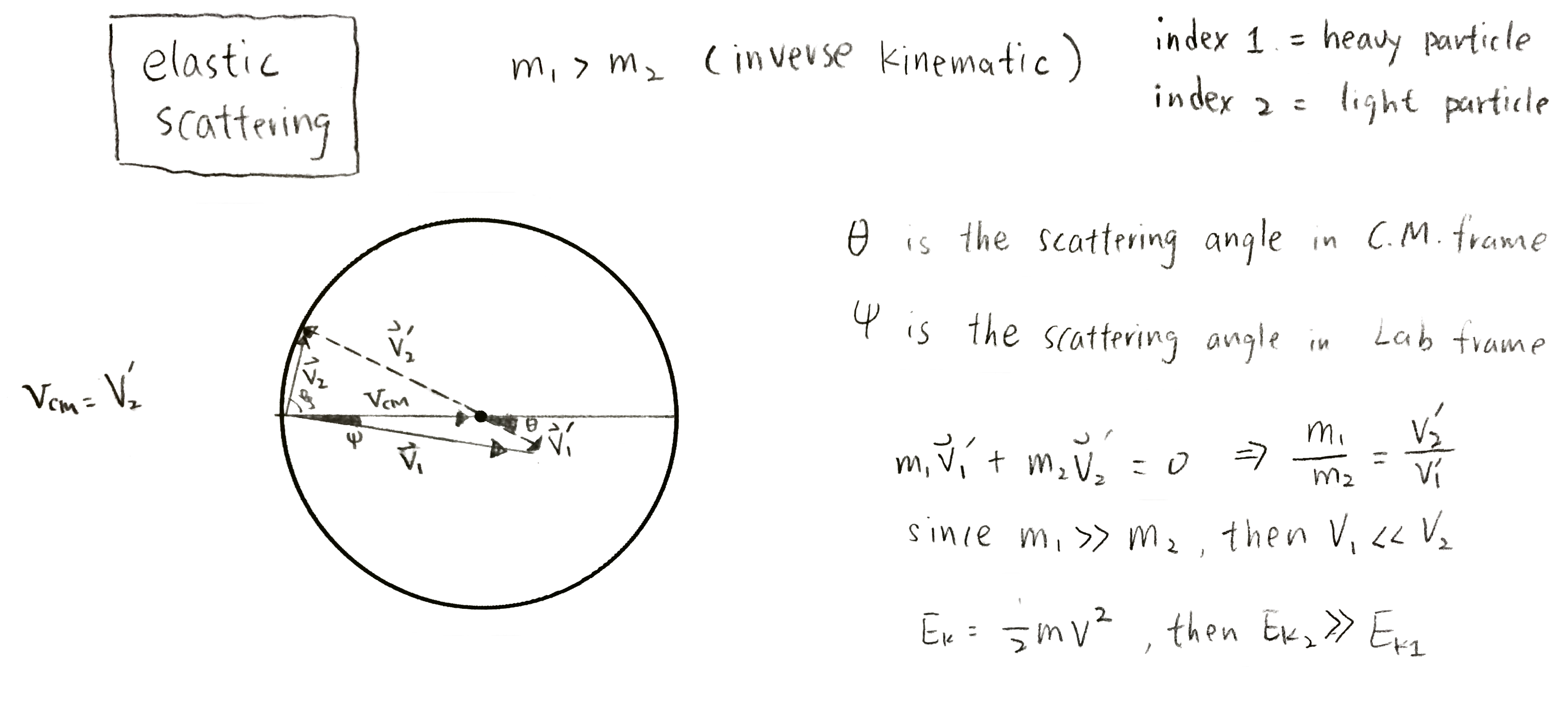
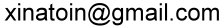Basic kinematics
The notations used here are following by the ones from the chapter 9 of the book "Classical Dynamics of Particles and Systems, 5th Edition" by Stephen T. Thornton and Jerry B. Marion. A notation with a prime indicates in the C.M. frame. $u$ is for the velocity before the reaction, $v$ is the velocity after the reaction. $m_1$ is the projectile(beam), $m_2$ is the target.
The characteristics for an elastic scattering:
- no mass and species change -> Q-value = 0; a(b,b)a
- In the C.M. frame each particle's magnitude of velocity does not change before and after reaction:
u'light_particle = v'light_particle, and u'heavy_particle = v'heavy_particle. - if the light particle is static before the scattering, then u'light_particle = Vcm; ( we call inverse kinematics).
if the heavy particle is static before the scattering, then u'heavy_particle = Vcm; ( we call normal kinematics) - $\theta$ is the "projectile" scattering angle in the C.M. frame, ranging from 0 to 180$^{\circ}$
- $\psi$ is the "projectile" scattering angle in the lab frame. $tan(\psi) = \frac{sin(\theta)} {cos(\theta) + m_1/m_2} $
- $\xi$ is the "target" scattering angle in the lab frame, and $\xi \lt$ 90$^\circ$, since $\xi = \frac{\pi}{2} - \frac{\theta}{2} $
( After the target get hit, the target will always go forward, in the Lab reference frame.)
Before reaction, $E_{CM} = \frac{1}{2} m_{1} u_{1}'^2 + \frac{1}{2} m_{2} u_{2}'^2$.
If the m2 is rest in the lab frame, $E_{Lab} = \frac{1}{2}m_1 u_{1}^2$, and $E_{CM} = E_{Lab} \cdot \frac{m2}{m1+m2} $
The characteristics for an inelastic scattering:
- no mass change and species change but Q-value < 0, since some part of the incoming particle's kinematic energy converts to the excitation energies, that is a(b,b)a*.
Note: Q value can be considered as $ Q = KE_{outgoing} - KE_{incoming}$.
The characteristics for the inverse kinematics:
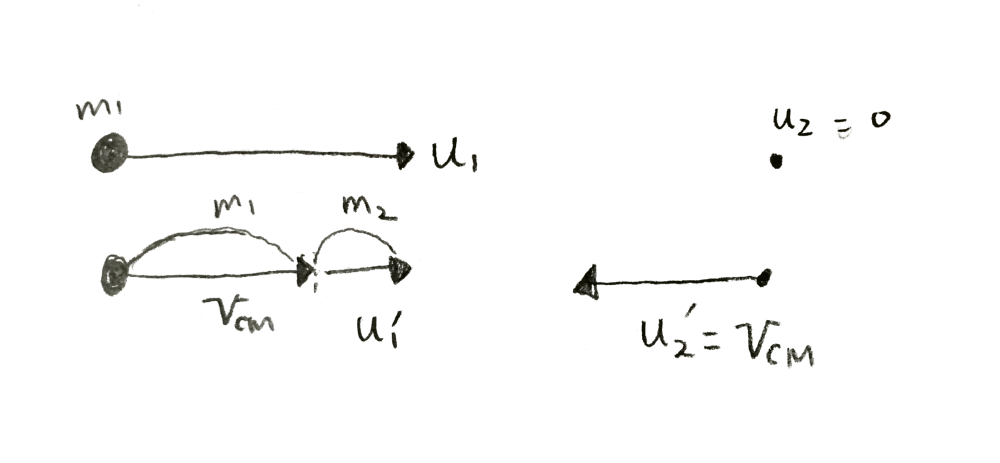
- m1 is the heavy particle, which is our beam. m2 is the light particle, which is our static target.
- u'heavy_particle < u'light_particle. (since $\vec{u}'_{heavy}\cdot m_{heavy} + \vec{u}'_{light}\cdot m_{light} = 0 $)
- Vcm ≈ uheavy_particle (=u1).
(since $V_{cm} = (m_{heavy}u_{heavy} + m_{light}u_{light})/(m_{heavy}+m_{light}) $, and $u_{light}=0$, $m_{heavy} >> m_{light} $) - u'light_particle = Vcm.
-
For an elastic scattering,
v'heavy_particle = u'heavy_particle , and
v'light_particle = u'light_particle = Vcm. and so
v'heavy_particle < v'light_particle. -
In the Lab frame, the scattering angle for the heavy particle, $\psi$, is small.
Since v'heavy_particle is small. vheavy_particle = Vcm + v'heavy_particle, will not change the direction much.
The direction of the heavy particle is almost along the beam line after reaction in the Lab frame.
- The smaller scattering θ will have higher cross sections,
i.e. the most counts for the light particle ( = target, in the inverse kinematics) appear at angle ξ ≈ 90 deg.
The characteristics for a transfer reaction in inverse kinematics $m_1 \gg m_2$:
- There will be non-zero Q-value, due to mass and species change.
- The mass ratio of the heavy particle changes very lightly, but for the light particle it changes dramatically.
- the heavy particle will be still similar to the elastic scattering after the reaction.
- pickup reaction, such as (p,d), mass of the light particle is double after the reaction.
-
for (p,d),
$u^{'}_{light} = V_{cm}$
( since the light particle is static before reaction in Lab frame, hence in the C.M. frame light particle moves by $V_{cm}$ toward the heavy particle. Before the reaction in C.M. frame, light particle's velocity is dominant)
$v^{'}_{light} \approx \frac{1}{2}u^{'}_{light} \lt V_{cm} $
( After the reaction, the mass of light particle becomes double, and thus velocity becomes half )
the smaller velocity leads the forward focus in the lab frame. - stripping reaction, such as (d,p), mass of the light particle is halved after the reaction.
-
for (d,p),
$u^{'}_{light} = V_{cm}$
$v^{'}_{light} \approx 2u^{'}_{light} \gt V_{cm} $
Most light particle will be in the backward focus in the lab frame.
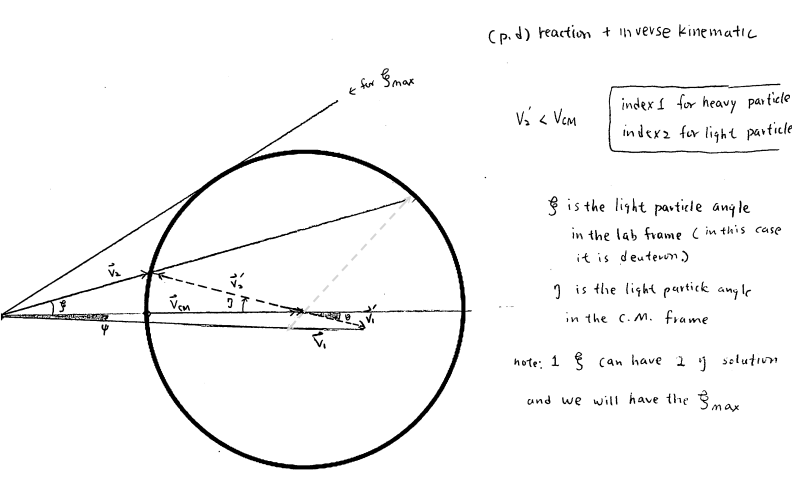
note: the length of the radius is $v^{'}_{2}$, i.e the velocity of the deuteron in the C.M. frame. And $V_{cm}$ is the vector from the point at the most left to the center of the circle. We can obviously see $V_{cm} \gt v^{'}_{2} $.
For a (p,d) reaction, we can have two solutions for a given Lab angle. One corresponds to the case where deuteron moves backward in the C.M. frame, whose $v_{2}$ is shorter, thus energy is less. Similarly, the case where deuteron move forward in the C.M. frame would have higher energy. In both cases, the deuteron "ALWAYS" moves forward in the Lab frame.
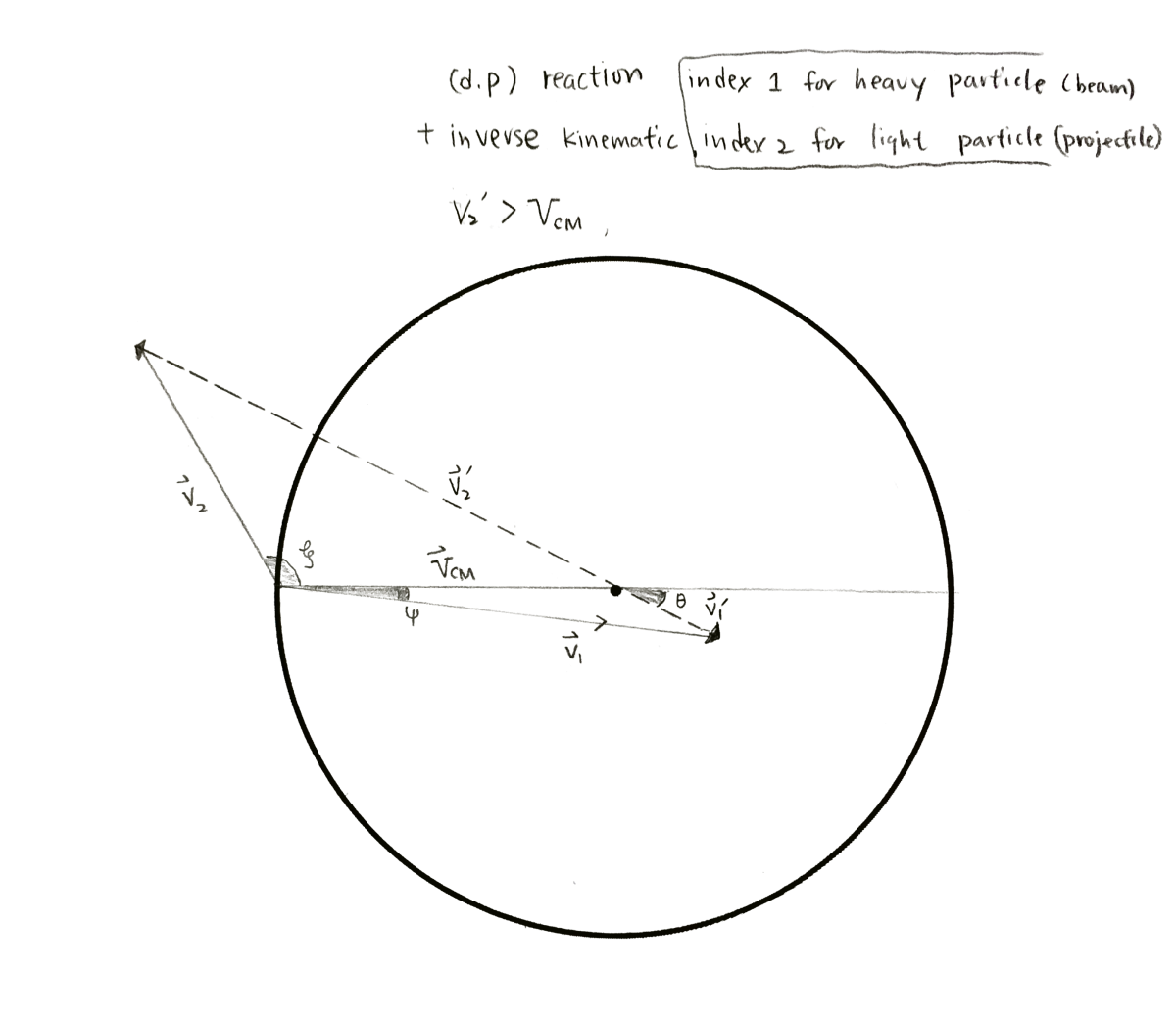
note: the length of the radius is $V_{cm}$, and $v^{'}_{2} \gt V_{cm}$.
$q = 1 + Q/KE_{cm}$
$Q = Q_{gs} - E_{x}$,
$KE_{cm} = $ total kinematic energy in the C.M. frame, mostly carried by light particle.
$f$ is the mass change ratio, $f = \frac{ m_{\,light\,before} }{ m_{\,light\,after} }$, for (d,p) reaction, $f \approx 2$.
Real case:
Suppose the beam is 132Sn ( m1 ≈ 132) and the target is deuteron d (m2 ≈ 2).
the beam energy of 132Sn is 5MeV/A, that is 660 MeV in total. Their mass ratio (m1/m2 ≈ 66).
In the lab frame, beam is moving with velocity u1. The target is static, and hence u2 = 0.
Vcm = 0.98 u1, is mostly equal to u1 for inverse kinematic reaction.
After the elastic scattering, no mass changes; the recoil is 132Sn, and the ejectile is also deuteron, and there is no excitation for both particles; Q-value =0. In the lab reference frame, the recoil of 132Sn has very small deviation off the beam axis. Its max scattering angle in the lab frame (ψ) is less than 1 deg.
In the lab reference frame, scattering angle (ξ) of the ejectile of d is always less than 90 deg,
that is always at the downstream of the beam direction; the forward angle. And it holds true for all elastic reactions that the ejectile is always less than 90 deg. And hence, several particle detector have more particle identification tools placed at the forward angle. Because they want to measure the elastic cross sections, which can be used as normalization.
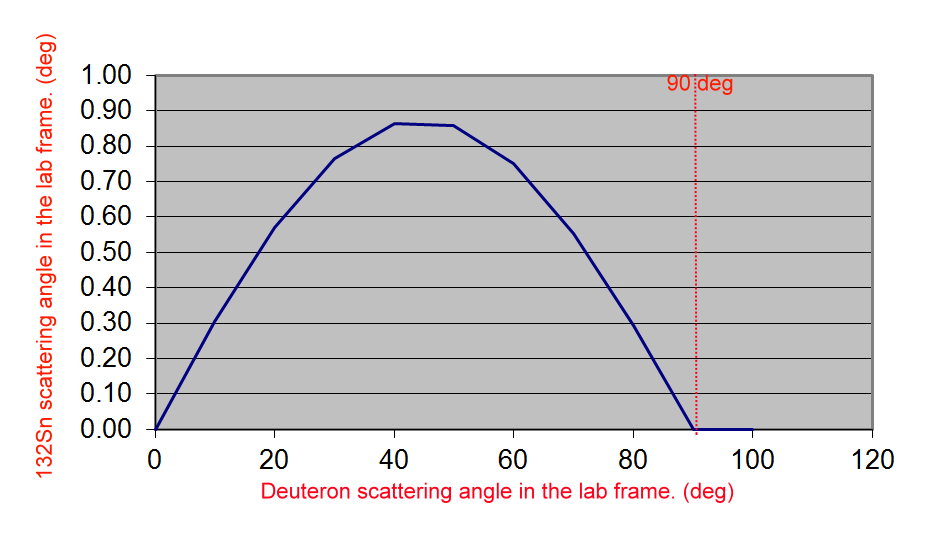
(Figure: calculations from CATKIN)
one more example (from Wilton N. Catford ):
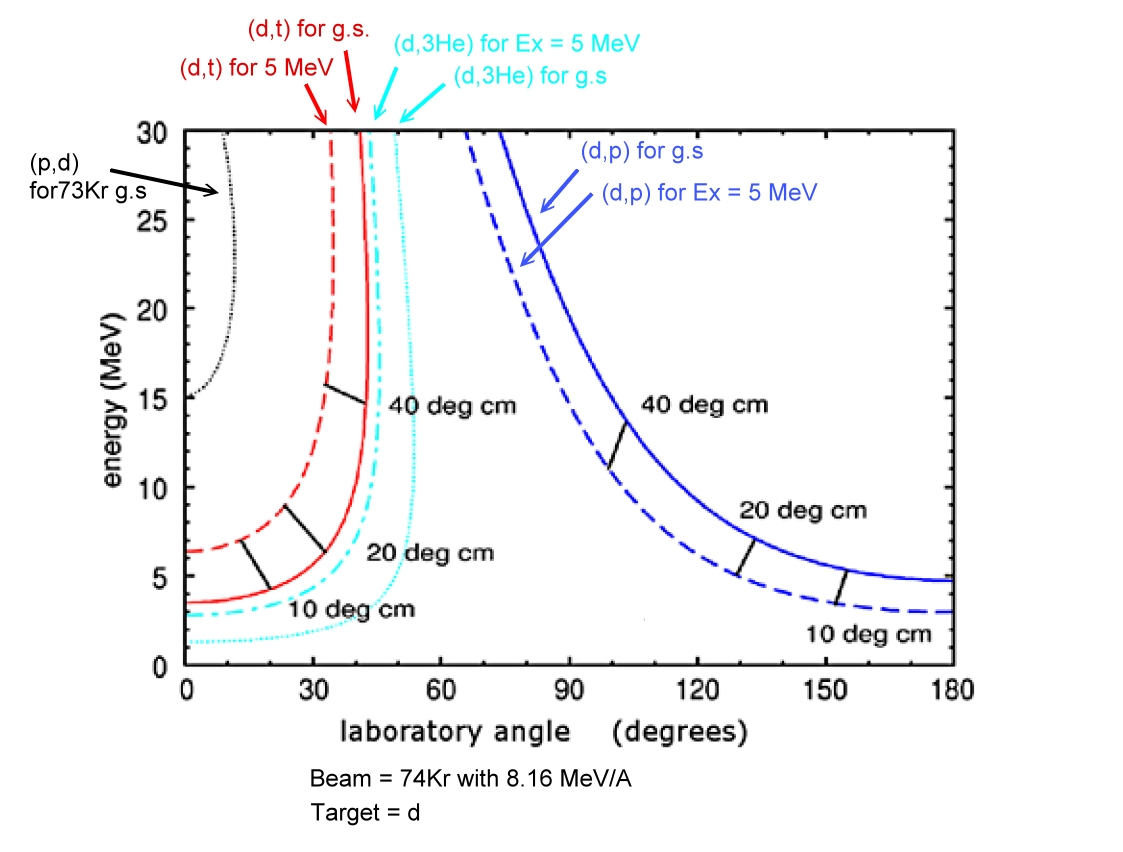
pickup reactions will be forward focus.
(d,3He) = get one more proton,
(p,d) and (d,t) = get one more neutron.
stripping reactions will be backward focus
(d,p) = lose one neutron.
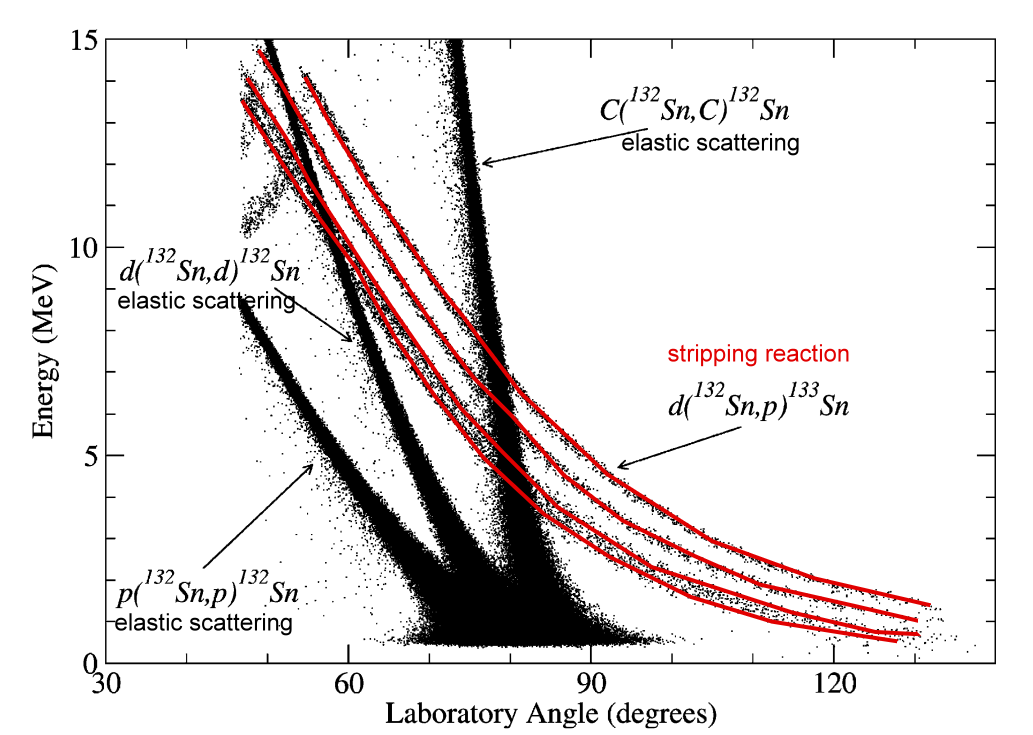
(Figure from http://dx.doi.org/10.1016/j.nimb.2007.04.289)
From experiment, we can measure the Energy of the particle and the lab frame angle.
We then can convert it to Q-value spectrum.
The formula can be found at the page 140 of "Nuclear Reaction Analysis" by Maryon Young
Or from this small site (here)
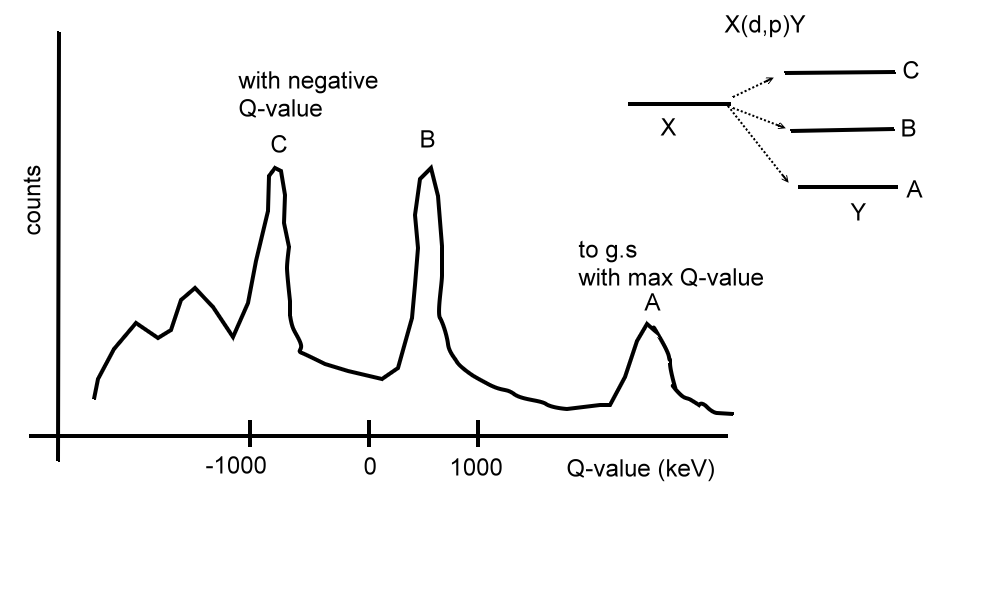
note for Q-value:
The Q-value can be negative,
since portion of energy is deposited to the higher excited state.
If the final products are all in the ground states, then Q value is simply the mass difference between those before and after a reaction.
$Q = (m_{target} + m_{beam})\cdot c^{2} - ( {m_{recoil} + m_{ejectile} )\cdot c^{2}}$
When its Q value is positive, then it means we we get extra energy after this reaction.
If its Q value is negative, we need to input energy it them to make this reaction happens. For example, we use an accelerator to accelerate the beam particle, such that the $E_{beam} + Q $ > 0, and the rest of energy distribute to $ E_{recoil} + E_{ejectile}$.
How about if the recoil is not in the ground state, but in its excited state?.
In this case, we need to have $E_{beam} + Q_{ground} - E_{x} $ > 0.
or we can define $Q_{E_{x}} = Q_{ground} - E_{x} $.
For example for 86Kr(p,d) 85Kr, reaction,
ground state Q value = -7.632 MeV,
the first excited state Q value = -7.632 - 0.304 = -7.936 MeV.